题外话
过年玩了下陶笛,入门真的很快🥳。 复刻了(毁原作)仙剑bgm回梦游仙 宝可梦未白镇 。这个网站不错,可以把陶笛的伴奏取出来
试吹下塞尔达的bgm
背景
摆烂到现在玩疯了,收收心准备毕业的事。其中用到了一个Metis工具包,它是一个串行图分割工具,可以用于将带权值的无向图进行平衡分割。该工具包非常经典,使用C/C++编写,使用教程1。
Metis官方手册了解些大概工作原理。官方手册中介绍Meis(机翻):
找到高度非结构化图的良好划分的算法对于在串行和并行计算机上为许多应用领域的广泛问题开发有效的解决方案至关重要。例如,在并行计算机上进行大规模数值模拟,例如那些基于有限元方法的数值模拟,需要将有限元网格分布到处理器上。这种分布必须使分配给每个处理器的元素数量相同,并且分配给不同处理器的相邻元素数量最小化。
第一个条件的目标是平衡处理器之间的计算。第二个条件的目标是最小化由于将相邻元素放置到不同处理器而导致的通信。图划分可以成功地满足这些条件,首先用图对有限元网格进行建模,然后将其划分为相等的部分。图划分算法也用于计算稀疏矩阵的填充减少顺序。当直接方法用于求解线性方程组的稀疏系统时,这些减少填充顺序是有用的。一个良好的稀疏矩阵的排序极大地减少了内存的数量以及解决方程组所需的时间。此外,由图划分算法产生的填充减少排序特别适合于并行直接分解,因为它们在分解阶段导致了高度的并发性。
图划分也用于解决许多领域出现的优化问题,如超大规模集成电路(VLSI)的设计、存储和访问磁盘上的空间数据库、运输管理和数据挖掘
Metis属于offline类型的边分割,基础图分割的知识介绍请看这篇博客2。 简言之,无向图的分割按照切割方式分为边分割(点分区)和点分割(边分区),即切割图时,来确定是切割的点或边。 其中一次性将图导入进行分区切割的属于静态offline类型,否则属于流式streaming类型。 流式的好处在于对于大规模的图处理所需的内存将更小。
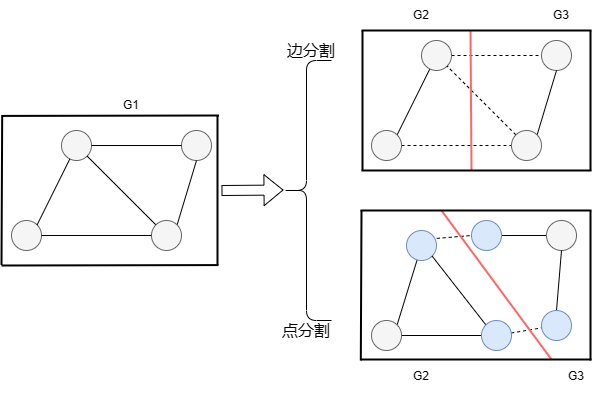
至于流式的图分割之类的,可以阅读这些文章3 4,本人只是应用实践,没有做深入研究。
实践
这里使用Python包装的pymetis进行网络图分割。
直接 pip install pymetis 即可安装。pymetis使用 pymetis.part_graph(part, xadj=xadj, adjncy=adjncy, eweights=eweights) 来将拓扑图进行分割。由于该包仅仅是metis的API封装,底层调用的都是原版的api,修改算法时需要直接修改metis代码,只是使用的话看看手册就行。
为了后续的图分割比较直观,我这里会通过 neworkx 包展示了,构建类my_graph。其可以随机生成自定义的确定生成节点个数、链路密度的网络拓扑。为了直观展示图链路权重,通过get_weight_dict将链路权重与其拓扑图长度正相关,拓扑图G将保存为gml格式,该图格式能够保存节点、链路权重。
图分割及构建
from functools import cmp_to_key
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import math, sys
import string, pymetis
class my_graph():
@classmethod
def get_weight_dict(self, edges, pos)-> list :
# 传入链路和节点位置 edges pos 根据距离 * 66 求整数输出权值 注意权值不可为0
return [ (i, j, max(math.floor(66 * math.hypot(pos[i][0] - pos[j][0], pos[i][1] - pos[j][1])), 1)) for i, j in edges]
@classmethod
def creat(self, node_count=8, radius = 0.3, seed = 1, weight=True, save_file:string=None) -> nx.Graph:
"""
@node_count 网络节点个数,在画布上随机生成这些节点的位置
@radius 网络节点连接阈值,当距离小于该值生成链路
@seed 随机种子
@weight 是否设定链路权值
@save 是否保存该邻接表数据
"""
# H = G.copy()
# https://en.wikipedia.org/wiki/Random_geometric_graph 生成随机图
G:nx.Graph = nx.random_geometric_graph(node_count, radius=radius, seed=seed)
if weight:
pos = nx.get_node_attributes(G, "pos")
# 按照距离计算并添加权重
G.add_weighted_edges_from(self.get_weight_dict(G.edges(), pos))
if save_file:
nx.write_gml(G, save_file)
self.G = G
return G
@classmethod
def get_csr_data(self, G:nx.Graph):
edges = [(i, j, G.adj[i][j]['weight']) for i,j in G.edges()]
edgesList = edges + [(j, i, w) for i, j, w in edges]# 链路有两种形式 12 21 这里手动复制一份
cmp = lambda t1,t2 : t1[1]-t2[1] if t1[0]==t2[0] else t1[0]-t2[0]
edgesList.sort(key = cmp_to_key(cmp)) # 按照元组前两个元素大小排下序
adjncy = [j for i,j,w in edgesList]
eweights = [w for i,j,w in edgesList]
xadj, xid = [0, ], 0 # 注意 xadj必须按照 节点 [0, n) 顺序读取,如果该节点不存在链路则新id下标不变
if not edgesList is []:
for i in range(1, len(edgesList)):
while xid < edgesList[i][0]:
xadj.append(i)
xid += 1
# if edgesList[i-1][0] != edgesList[i][0]: # 这样会遗漏没有链路的节点
# xadj.append(i)
xadj.append(len(edgesList)) #len(adj) == len(edgesList)+1
return (xadj, adjncy, eweights)
@classmethod
def mypart_graph(self, G:nx.Graph, part = 3):
xadj, adjncy, eweights = my_graph.get_csr_data(G)
n_cuts, membership = pymetis.part_graph(part, xadj=xadj, adjncy=adjncy, eweights=eweights)
nodes_parts = []
for p in range(part):
nodes_parts.append(np.argwhere(np.array(membership) == p).ravel())
print(f" xadj = {xadj}\n adjncy = {adjncy}\n edgesList = {eweights}") #分区验证打印 for debug
print(f"n_cuts: {n_cuts}, membership: {membership}, nodes_parts:{nodes_parts}")
return nodes_parts
图绘制
普通无向拓扑图及其邻接矩阵如下所示:
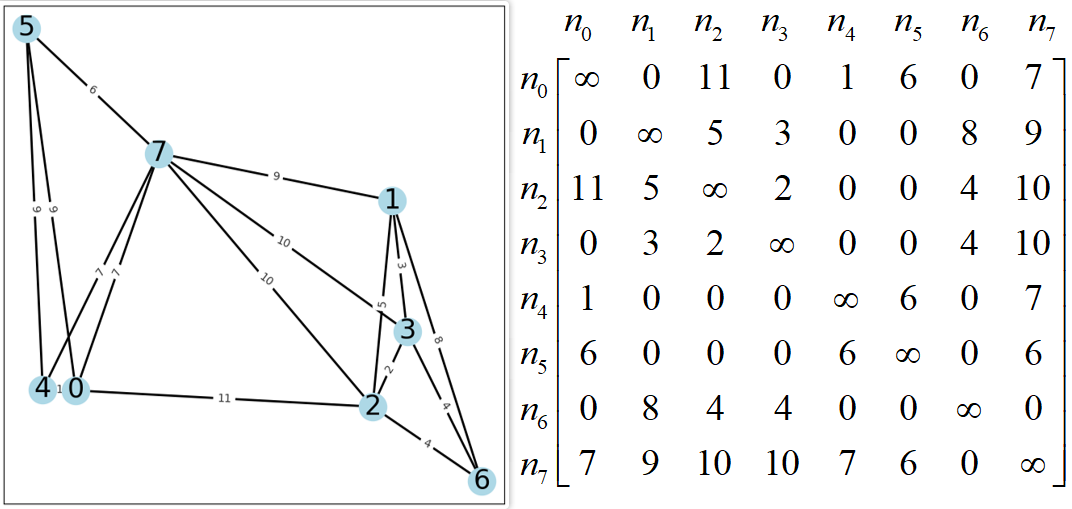
显然,使用邻接矩阵存储的边权有一半以上的重复空间,所以metis将图G=(V,E)压缩为CSR格式来进行处理,其包含4个数组:xadj、adjncy来描述图的拓扑,adjwgt与adjncy绑定顺序存储边权重、vwgt数组下标对应顶点序号存储点权重。这里使用get_csr_data来将图G转化为CSR格式。
vwgt = [1,1,1,1,1,1,1,1]
xadj = [0,4,8,13,17,20,23,26,32]
adjncy = [2,4,5,7,2,3,6,7,0,1,3,6,7,1,2,6,7,0,5,7,0,4,7,1,2,3,0,1,2,3,4,5]
adjwgt = [11,1,9,7,5,3,8,9,11,5,2,4,10,3,2,4,10,1,9,7,9,9,6,8,4,4,7,9,10,10,7,6]
adjncy每一位储存拓扑图的目的节点序号,其对应边权重存储于adjwgt,adjncy值代表相连的目的节点序号,源节点默认从0开始。而源节点的切换就是由xadj来决定的。例如此图中,xadj第1个元素为0,第2个元素为4(首元素固有存在,该数组大小为节点数n+1),说明adjncy中下标从0到3的边的源节点都是0,目的节点为值2,4,5,权重为11,1,9。xadj第3个元素为8说明adjncy下标4到7的边源节点为1,目的节点为数组值,之后的值类比即可。其中需要注意,当某个节点不存在将其权重设置为0,节点相邻边不存在时要将adjncy相邻节点置为相同值,不能直接跳过该点。
注意转换CSR时 n1-n2 与n2-n1 链路双向都要考虑,我这里演示是直接将network的图G进行转换,这里根据你用途自己改。
至于函数 mypart_graph 就是调用metis原有api进行分割,METIS_PartGraphRecursive是多层级递归划分API,而METIS_PartGraphKway是多层级K-way划分。前者适合网络分区小于8,否则适用后者。pymetis的part_graph函数中的recursive参数bool也是根据分区是否大于8这个值来确定具体的分割api,可以自己传入。如果有想优化metis或对部分功能修改,可以去 pymetis_code/src/metis/* 中修改源码,进行make编译新代码会自动重新安装pymetis指定库。
后面就使用network的draw相关模块绘制下,上述的随机拓扑分区结果吧。
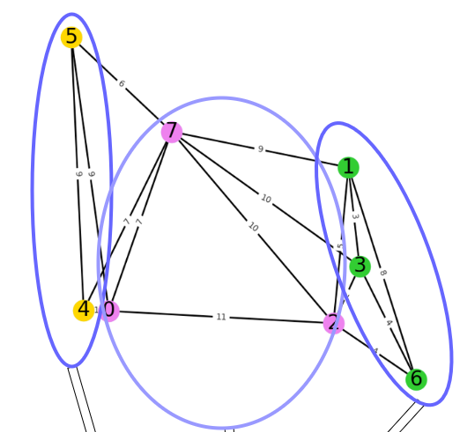
绘制网络图的类代码:
class graph_draw():
"""
by@lk233 设计了基础的 保存 解析的网络图类,绘制完毕后使用 plt.show() 即可
"""
def __init__(self, G=None, path:string=None) -> None:
"""
初始化该类需要传入 plt的绘制坐标系ax
若传入了路径则解析该路径邻接表 否则使用传入的G
"""
self.G = G
if not path is None:
self.G=nx.read_gml(path, label="id") #默认解析lable 得出的是str
def getG(self):
return self.G
def draw(self, ax, enable_lable=True, fs=6, ns=50, w=0.4) -> None:
# Draw the route
G:nx.Graph = self.G
pos = nx.get_node_attributes(G, "pos")
weight_labels = {(u, v): str(d["weight"]) for u, v, d in G.edges.data()}
if enable_lable:
G.edges.data
nx.draw_networkx_edge_labels(
G,
pos,
ax=ax,
edge_labels=weight_labels, # 将(n1 n2 w)形式的权重转lable传入
alpha=0.8,
font_size=10, #大图不推荐画权重
)
nx.draw_networkx(
G,
pos,
ax = ax,
with_labels=True,
node_shape='o', #定义节点形状
font_size=fs, #节点标号size #上百节点大图推荐值
# font_size=24, #节点标号size #小图用
# node_color='white',
node_color='lightblue',
edge_color="black",
# alpha=0.5, #透明度
node_size=ns, #节点size #上百节点大图推荐值4
# node_size=600, #节点size #小图用
# linewidths=4,
width=w,
)
# 按照颜色划分分区
def draw_node(self, ax, node_lists, ns):
node_color = ["gold", "limegreen", "violet", "yellow", "blue",
"green", "olive", "darkorange", "red", "grey"]
G:nx.Graph = self.G
index = 0
for nodelist in node_lists:
print(nodelist, node_color[index])
nx.draw_networkx_nodes(G,
nx.get_node_attributes(G, "pos"),
ax = ax,
nodelist=nodelist,
node_size=ns,
node_color=node_color[index])
index = (index + 1) % len(node_color)
matlab绘制颜色参考:

测试及调用代码
def mytest_csr():
fig = plt.figure(figsize=(12,6))
ax = plt.subplot()
G:nx.Graph = nx.Graph()
G.add_edge(0, 1, weight=0.6)
G.add_edge(0, 2, weight=0.2)
G.add_edge(0, 3, weight=0.3)
G.add_edge(2, 3, weight=0.1)
G.add_edge(2, 4, weight=0.7)
G.add_edge(2, 5, weight=0.9)
pos = nx.spring_layout(G, seed=7)
nx.set_node_attributes(G, pos, "pos")
xadj, adjncy, eweights = my_graph.get_csr_data(G)
print(f" xadj = {xadj}\n adjncy = {adjncy}\n edgesList = {eweights}")
mydraw = graph_draw(G=G)
mydraw.draw(ax)
plt.show()
exit()=
if __name__ == "__main__":
# mytest_csr() # 创建图 测试G转换CSR的正确性
ps = 3 # 分区数量
node_count = 2000# 节点数量
radius = 0.05 # 点之间距离阈值 两点间链路大于该值不产生链路
seed = 100 # 随机种子
fs = 4 # 节点id大小 4 24
ns = 60 # 节点图标大小 60 600
w = 0.4 # 链路粗细 0.4
flag = False # 是否绘制线权重 大图不推荐画权重
save_file = f"node_count{node_count}_{seed}"
read_flag = len(sys.argv) > 1
if read_flag:
print("read gml: save_file")
save_file = sys.argv[1]
mydraw = graph_draw(path=save_file)
else :
mydraw = graph_draw(
G=my_graph.creat(node_count, radius, seed, save_file=save_file+".gml"))
G = mydraw.getG()
# 绘制在一张图上
# ax1 = plt.subplot(2,1,1)
# ax2 = plt.subplot(2,1,2)
fig = plt.figure(figsize=(8,8))
ax1 = plt.subplot()
fig = plt.figure(figsize=(8,8))
ax2 = plt.subplot()
mydraw.draw(ax1, enable_lable=flag, fs=fs, ns=ns, w=w) #原拓扑图
mydraw.draw(ax2, enable_lable=flag, fs=fs, ns=ns, w=w) #新拓扑图
mydraw.draw_node(ax2, my_graph.mypart_graph(G, part=ps), ns=ns)
plt.show()
总结
1000节点分割结果展示,不同颜色代表不同分区:


当然也可以采用基于MPI的并行metis,也有封装包mgmetis可以用,不得不感叹python比c++编码快太多了,性能上也还行,之前串行的2000节点加上打印信息不到1s就绘制完了。用C++写可能我现在还在做图形化的工作。。。
回廊识路. 图划分软件Metis的使用–知乎 图划分软件Metis的使用 ↩︎
paradise. 图分割Graph Partitioning技术总结-知乎 图分割Graph Partitioning技术总结 ↩︎
骑士. 流式图分割–骑士的个人站点 流式图分割 ↩︎
吃橘子趁早. 动态图划分复制算法:Leopard–知乎 动态图划分复制算法:Leopard ↩︎
