并查集

并查集是一种树形的数据结构，用于处理不交集（Disjoint sets）的合并和查询问题。

案例：初始状态n个元素，每个元素位于独立的集合，之后进行合并操作将集合合并。合并过程中判断集合中是否有重复元素。

所以并查集主要的两个操作：

• 查询: find 确定某个元素处于哪个子集
• 合并: union 将两个子集合合并成一个集合

并查集的实现

思路:使用数组等结构记录每一个节点的父节点，查询操作就是递归的查询该节点的父节点找寻其root，合并操作就是把两个节点的中一个作为另一个节点的父节点这样就完成了合并。

一开始每个节点就是一个集合，随着所有节点迭代下去的合并，合并两个节点就相当于合并包含该节点的两个集合。每两个节点合并时查询两个节点的的root节点。如果相同说明两个这两个集合有相同的子节点，合并后必定会产生环。

优化：

• 路径压缩：查找root节点的时候就直接把他的父节点改为root，省的下次重复查找
• 按秩合并：维护一个秩数组，记录该节点下的子树深度。这样合并两个节点时，让秩大的做父节点避免子树过长。

视频的解析很清楚，做个提纲防止忘记

视频的源码：

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

#define VERTICES 6
#define _CRT_SECURE_NO_WARNINGS
int find_root(int x, int parent[])  // 找到根节点
{
    if (parent[x] != x) {      //当父节点是自己说明已经是根节点
        parent[x] = find_root(parent[x], parent); //路径压缩,找父节点的同时更新自己的父节点为root节点
    }
    return parent[x];
}
int union_vertices(int x, int y, int parent[],int rank[])  // 让两个集合合并
{
    int x_root = find_root(x, parent);
    int y_root = find_root(y, parent);
    if (x_root == y_root)
        return 0;
    else {
        if (rank[x_root] > rank[y_root])  // 让 少的指向多 的
            parent[y_root] = x_root;
        else if (rank[x_root] < rank[y_root])
            parent[x_root] = y_root;
        else {
            parent[x_root] = y_root;   // 这个随便可以
            rank[y_root]++;
        }
        return 1;
    }
}

int main(void)
{
    int parent[VERTICES] = { 0 };
    int rank[VERTICES] = { 0 };
    memset(rank, 0, sizeof(rank));
    // memset(parent, -1, sizeof(parent));
    for (int i = 0; i < VERTICES; i++) //初始父节点就是自己
        parent[i] = i;
    int edges[6][2] = { {0,1},{1,2},{1,3},{2,4},{3,4},{2,5} };

    for (int i = 0; i < 6; i++) {
        int x = edges[i][0];
        int y = edges[i][1];
        if (union_vertices(x, y, parent,rank) == 0)
        {
            printf("Cycle detected!\n");
            system("pause");
            exit(0);
        }
    }
    printf("No cycle found.\n");
    system("pause");
    return 0;
}

并查集的应用

leetcode 547题目

class Solution {
public:
    int find(int i) {
        if (parent[i] != i) //递归寻找root节点并把root赋值
            parent[i] = find(parent[i]);
        return parent[i];
    }
    void merge(int i, int j) {
        int root1 = find(i), root2 = find(j);
        if(root1 == root2)  // 若相等则两个集合有交集，相当于在同一个省份内的两个城市相连（成环）
            return;         // 这里不做任何处理 ans省份树不会减少
        ans--;  // 接下来进行合并
        if(rank[root1] >= rank[root2])
            parent[root2] = root1;
        else
            parent[root1] = root2;
        if (rank[root1] == rank[root2])
            rank[root1]++;
    }

    int ans;
    vector<int> parent, rank;
    int findCircleNum(vector<vector<int>>& isConnected) {
        ans = isConnected.size();   //初始视作每个城市都是一个省份
        rank.resize(ans, 0);
        for (int i = 0; i < isConnected.size(); i++)
            parent.push_back(i);
        for (int i = 0; i < isConnected.size(); i++) {
            for (int j = 0; j < isConnected.size(); j++) {
                if (isConnected[i][j] == 0 || i == j)
                    continue;
                merge(i, j);
            }
        }
        return ans;
    }
};

题外话：双指针判断链表是否有环，看起来类似也是找环，但是用的双指针找的。141. 环形链表

堆

这里说的堆指的时数据结构堆，不是程序申请的堆空间。

堆（heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。

堆总是满足下列性质：

• 小根堆Min-heap: 父节点的值小于或等于子节点的值； 大根堆Max-heap: 父节点的值大于或等于子节点的值；

• 堆中某个结点的值总是不大于或不小于其父结点的值；

• 堆总是一棵完全二叉树¹

  其插入添加元素的时间复杂度都为O(log n)。查询最大、小值的时间复杂度为O(1)

堆的实现

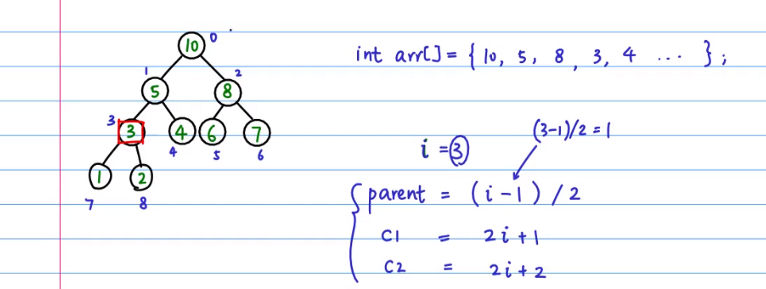
由于堆是一颗完全二叉树，所以完全可以用一个数组准确并唯一的表示该二叉树。

用数组表示该完全二叉树由上到下、由做到右的记录时，有以下性质：

• 父节点 = (i - 1) / 2
• 左子节点 = 2 * i + 1
• 右子节点 = 2 * i + 2

C++ STL库优先队列的使用方式

头文件: #include <queue>

priority_queue<point, vector<point>, greater<point>> que;
// 第一个参数是存储对象的类型，第二个参数是存储元素的底层容器，第三个参数是函数对象，第二第三参数可以不填入
// 与sort刚好相优先队列反队列默认采用的是less生成的是大根堆，sort 默认是 less 从小到大升序排序

堆的应用

用于堆排序 时间复杂度O(nlog n)，额外空间复杂度O(1)

// 对一个节点做heapify的时候，必须保证它的所有子树都已经是堆。  
void swap(int *a, int *b) {
    int temp = *b;
    *b = *a;
    *a = temp;
}
void max_heapify(int arr[], int start, int end) {
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end) { 
        if (son + 1 <= end && arr[son] < arr[son + 1]) // 判断右子节点是否存在，并比较大小
            son++;
        if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕，直接跳出函數
            return;
        else { // 否则交换父子节点
            swap(&arr[dad], &arr[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}
void heap_sort(int arr[], int len) {
    int i;
    // 初始化，从最后一个父节点开始调整
    for (i = (len-2) / 2; i >= 0; i--)
        max_heapify(arr, i, len - 1);
    // 取出最大值(堆头)，然后重新heapify  这里优化为将堆头换到最后一位，然后最后一个节点不参加heapify
    // 迭代全部堆头后，就是排序后的列表
    for (i = len - 1; i > 0; i--) {
        swap(&arr[0], &arr[i]);
        max_heapify(arr, 0, i - 1);
    }
}

用优先队列解决的案例：23. 合并K个升序链表 - 力扣（LeetCode） (leetcode-cn.com)

    class Solution {
    public:
        //题目23  "重载结构体的<"，用默认的less（所以省略了该参数）
        struct Status {
            int val;
            ListNode *ptr;
            bool operator < (const Status &rhs) const {
                return val > rhs.val;
            }
        };
        priority_queue <Status> q;

        ListNode* mergeKLists(vector<ListNode*>& lists) {
            for (auto node: lists) {
                if (node) q.push({node->val, node});
            }
            ListNode head, *tail = &head;
            while (!q.empty()) {
                auto f = q.top(); q.pop();
                tail->next = f.ptr; 
                tail = tail->next;
                if (f.ptr->next) q.push({f.ptr->next->val, f.ptr->next});
            }
            return head.next;
        }
    };

    // "也可以重载()" 其实 greater 和 less 就是一个模板调用的模板类，里面重载了元素的() 返回> 或<的bool
    // STRUCT TEMPLATE greater
    template <class _Ty = void>
    struct greater {
        _CXX17_DEPRECATE_ADAPTOR_TYPEDEFS typedef _Ty _FIRST_ARGUMENT_TYPE_NAME;
        _CXX17_DEPRECATE_ADAPTOR_TYPEDEFS typedef _Ty _SECOND_ARGUMENT_TYPE_NAME;
        _CXX17_DEPRECATE_ADAPTOR_TYPEDEFS typedef bool _RESULT_TYPE_NAME;

        _NODISCARD constexpr bool operator()(const _Ty& _Left, const _Ty& _Right) const {
            return _Left > _Right;
        }
    };
    // 重载()如下所示
    struct com{
        bool operator()(pair<int,int>&a,pair<int,int>&b){
            return a.second>b.second;
        }
    };
    priority_queue<pair<int,int>,vector<pair<int,int>>,com> q;