常用小技巧
leetcode刷题遇到的一些问题,关于算法的结构文字描述的有限,记录些常用的单元的代码,备忘。
防止溢出求平均数
一般求平均数时会 (a+b)/2 或 (a+b)>>1 来做,但是若数较大时 a + b 会出现溢出情况,可以使用以下几种方法来做:
c = a + (b - a) / 2;a&b + ((a^b) >> 1 )
a&b : 获取两个数同为1的位
a^b: 获取两个数不同为1的位
两个数的平均值为两个数的每一位平均值的和
最小公倍数 最大公约数
利用最大公约数求最小公倍数
定理: 已知a,b最大公约数为X,最小公倍数为Y,则有公式为a*b=最大公约数X * 最小公倍数Y
证明:由已知得a=Xc b=Xd 且c与d互为素数(否则X就不是c与d的最大公因数)所以Y=Xcd, 即a*b = c * X * X * d = X * Y
辗转相除法求最大公约数: 用较大数除以较小数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。如果是求两个数的最大公约数,那么最后的除数就是这两个数的最大公约数
定理:两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。最大公约数(Greatest Common Divisor)缩写为GCD。gcd(a,b) = gcd(b,a mod b) (不妨设a>b 且r=a mod b ,r不为0)
证明: a可以表示成a = kb + r(a,b,k,r皆为正整数,且r<b),则r = a mod b 假设d是a,b的一个公约数,记作d|a,d|b,即a和b都可以被d整除。 而r = a - kb,两边同时除以d,r/d=a/d-kb/d=m,由等式右边可知m为整数, 因此d也是b,a mod b的公约数。(a,b)和(b,a mod b)的公约数相等,则其最大公约数也相等,得证。
int MinBei(int a, int b) {
int tmp, count = a * b;
// 求最大公约数 迭代写法
while (b) {
tmp = b;
b = a % b;
a = tmp;
}
return count / a ;
//两数相乘等于 最大公约数乘最小公倍数
}
// 求最大公约数的递归写法
int gcd (int a, int b) {
return b ? gcd(b, a % b) : a;
}
int main()
{
int a, b, c, temp;
cin >> a >> b >> c;
temp = MiniBei(a, b);
// cout << temp << endl;
temp = MiniBei(c, temp);
// cout << temp << endl;
cout << temp;
return 0;
}
质(因)数
哥德巴赫猜想:任一大于2的偶数,都可表示成两个素数之和。
合数性质:
- 所有大于2的偶数都是合数,也就是在正整数中除了2以外,其余数的个位数为0、2、4、6、8者均为合数。4为最小的合数。
- 每一合数都可以以唯一形式被写成质数的乘积。(算术基本定理)
- 所有合数都有至少3个正因数,例如4有正因数1、2、4,6有正因数1、2、3、6。
- 对任一大于5的合数n,(n-1)!==0(威尔逊定理)
- 对于任意的正整数n,都可以找到一个正整数x,使得x、x+1、x+2、…、x+n 都是合数。
快速计算是否为质数方法:
根据性质2,任何一个合数都能能分解成质数相乘,那么可以表示为N=a1*a2*...*ak,(ak均为质数)
上述质因数拆分中 k >= 2,所以最小质因数为a1,容易知道a1小于 sqrt(N)
即合数一定存在一个小于sqrt(N)的质因数
6x 6x-2 6x-3 6x-4肯定不是质数。
所以如果 n 是6 倍数两侧的数,那么n才有可能是质数。
即结论 质数(大于3时)一定是6x-1 或6x-5(x>=1)
#include <iostream>
#include <cmath>
// 最原始
bool isPrime(int n){
if (n <= 3) {
return n > 1;
}
for(int i = 2; i < n; i++){
if (n % i == 0) {
return false;
}
}
return true;
}
// 初步优化
// 若不是质数 其一定存在因数p1<=sqrt(n),p2>=sqrt(n)
bool isPrime1(int n) {
if (n <= 3) {
return n > 1;
}
int s = (int)sqrt(n);
for (int i = 2; i <= s; i++) {
if(n % i == 0) {
return false;
}
}
return true;
}
// 质数还有一个特点,就是它总是等于 6x-1 或者 6x-5,其中 x 是大于等于1的自然数。
bool isPrime2(int num) {
if (num <= 3) {
return num > 1;
}
// 不在6的倍数两侧的一定不是质数
if (num % 6 != 1 && num % 6 != 5) {
return false;
}
int s = (int)sqrt(num);
// 若这个数是合数,则必有质因数i,i <= sqrt(num)
// 且i为质数一定为6倍数两侧,以6为步长寻找
// 寻找在 根号n 内是否存在 类似因数 6i+1 6i+5
for (int i = 6; i <= s; i += 6) {
if (num % (i-1) == 0 || num % (i+1) == 0) {
return false;
}
}
return true;
}
若是求范围内质数的个数 则可以用这个方法求解
其原理也十分易懂:从1到n遍历,假设当前遍历到m,则把所有小于n的、且是m的倍数的整数标为和数;
遍历完成后,没有被标为和数的数字即为质数。
// 求 [1,n) 范围内质数个数 可以采用此方法
int countPrimes(int n) {
if (n <= 2) return 0;
vector<bool> prime(n, true) ;
int count = n - 2; //去掉不是质数的1 和范围外的n
for(int i = 2; i < n; ++i){
if (prime[i]) {
for (int j = 2*i; j < n; j += i){ // 将i的整数倍删除
if (prime[j]) {
prime[j] = false;
--count;
}
}
}
}
return count;
}
// 优化版本
int countPrimes1(int n) {
if (n <= 2) return 0;
vector<bool> prime(n, true);
int i = 3, sqrtn = sqrt(n), count = n / 2; // i>=3的偶数一定不是质数
for (int i = 3; i <= sqrtn; i+=2) {
if(prime[i]) {
// 只对当前是未被标记的质数才进行 平方后累加2i的数设定为合数 减少重复遍历
// i为3开始的奇数 进入合数统计时 +i必定为偶数数没必要遍历 已经提前把偶数个数减少了
for (int j = i*i; j < n; j += 2*i){
// j不断 + 2i 为了避免偶数 的遍历
if (prime[j]) {
--count ;
prime[j] = false;
}
}
}
}
return count;
}
平方根函数
用牛顿法实现快速求平方根的近似函数。
计算机通常使用循环来计算 x 的平方根。从某个猜测的值 z 开始,我们可以根据 z² 与 x 的近似度来调整 z,产生一个更好的猜测:
z -= (z * z - x) / (2*z)
上面的 z² − x 是 z² 到它所要到达的值(即 x)的距离, 除以的 2z 为 z² 的导数,我们通过 z² 的变化速度来改变 z 的调整量。X在上式中为固定值。
当求A的平方根时 设f(x) = x^2
上问题即为求 f(x) = A的解
构造函数 F(X) = f(x) - A = x^2 - A
A为所求的常数 用牛顿法求解不断迭代下去 直到 Xn+1 与 Xn 差值足够小
即迭代求 Xn+1 = Xn - F(Xn) / F’(Xn)
这种通用方法——牛顿法。 它对很多函数,特别是平方根而言非常有效。
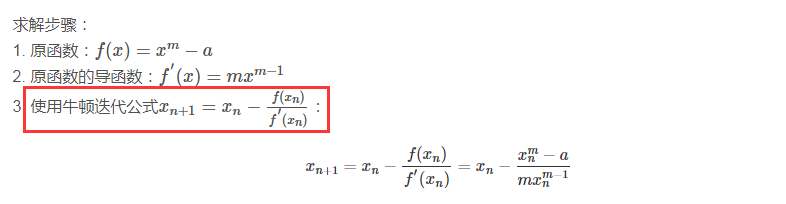
int main()
{
double x1, x2;
float a;
scanf("%f", &a);
x2 = 1.0;
do
{
x1 = x2;
x2 = (x1 + a / x1) / 2;
// x2 -= (x2 + a / x2) / 2; 也可如此简写
} while (fabs(x1-x2)>pow(10,-5));
// } while (fabs(x1-x2) > 1e-5);
printf("value:%lf", x2);
system("pause");
return 0;
}
扩展,雷神之锤源码平方根调用方法,只看最后一部分即可。将 f(x)=y 转为 f(y)=x 来简化运算
回文数
求回文时,若是字符串就法1比较,若是数字利用迭代乘、余来做
// 法1
while (start < end) {
if (nums[start++] != nums[end--])
return false;
}
return true;
//法2
bool isPalindrome(int x) {
if (x < 0 || (x % 10 == 0 && x != 0))
return false;
int revertedNumber = 0;
while (x > revertedNumber) {
revertedNumber = revertedNumber * 10 + x % 10;
x /= 10;
}
// 当数字长度为奇数时,我们可以通过 revertedNumber/10 去除处于中位的数字。
// 例如,当输入为 12321 时,在 while 循环的末尾我们可以得到 x = 12,revertedNumber = 123,
// 由于处于中位的数字不影响回文(它总是与自己相等),所以我们可以简单地将其去除。
return x == revertedNumber || x == revertedNumber / 10;
}
位运算
注意:左移运算用零填充右边空缺的bit位,无符号数的右移运算也是用0填充左边空缺的bit位,但是有符号数的右移运算会用符号位的值填充左边空缺的bit位。
因为这个原因,最好用无符号运算,这样你可以将整数完全当作一个bit位模式处理。
| ! | 逻辑非 |
|---|---|
| ~ | 位非 |
| ^ | 异或 |
| | | 或 |
| & | 与 |
| 功能 | 使用方法 | 参考链接 |
|---|---|---|
| 树状数组中的求 一个数二进制的1的最低位置 | 直接 return = x&(-x) | lowbit 树状数组关键函数 |
| 求某个数据出现次数 | 使用 &操作,复杂的添加状态表 | https://leetcode-cn.com/problems/single-number/ |
| 将x的最低的一个非零的bit位清零 | 使用 x&(x-1) | |
| 查询一个64位数据的二进制1个数 | 建表查,省的每次都循环64次 | 右边main文件内含建表代码 |
| 移位查数据,除了直接 » 也可如右边 | x&(1«i) |
标准二分查找及其衍生
//二分法查找/折半查找
int binarySearch(Element array[], int len, int key){
int low = 0, high = len - 1, middle;
while(low <= high){
middle = (low + high) / 2;
if(array[middle] == key){ //找到,返回下标索引值
return middle;
}else if(array[middle] > key){ //查找值在低半区
high = middle - 1;
}else{ //查找值在高半区
low = middle + 1;
}
}
return -1; //找不到
}
std库 lower_bound 寻找第一个大于等于num的值的下标 自实现 (未添加 超出上下限的判断):
int mylower_bound(int* array ,int size,int key){
int first = 0, middle ,last = size-1;
while(first<last){
middle = (first+last) >> 1;
if(array[middle] <key ) //当middle小于要找的位置 , first +1 也不会超过key的位置,最多相同
first = middle + 1;
else
last = middle ; //middle有可能等于要找的位置 , last = middle , 用first不断逼近
}
return first;
}
// 有重复数据也可排出结果 可以返回值范围为 0-size
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int l = 0, r = nums.size()-1;
while(l <= r) {
int mid = (l + r) >> 1;
if(nums[mid] < target)
l = mid+1;
else
r = mid-1;
}
return l;
}
};
